20.4. ベクトルの計算と関数の図示

数学関数やデータをグラフに描く方法について、入門部分を紹介します。

ここで紹介するベクトルは、線形代数のベクトルとしても使えますが、このページでは一定の長さの実数の列としてのみ使います。

数学関数の図示 #

例として、ニューラルネットワークの訓練などでたまに登場するsoftplus関数を紹介します。 この関数は次の式で定義されます。

$\sigma_+(a)=\log(1+e^a)$ この関数がどのような性質を持つかは、右図のグラフを見ると一目で分かることでしょう。

計算機がこのようなグラフを描く際には、 $x$ の範囲を決め、その範囲で $x$ の値をいくつかサンプルし (たとえば $(0, 1, 2)$ )、 対応する $y$ の値を計算し (同 $(f(0), f(1), f(2))$ )、全体を滑らかにつなげるという手順を踏みます。

そこで x 座標の列をまとめて扱う方法、対応する y の列をまとめて計算する方法、最後にグラフを描く方法の順で紹介します。

ベクトルの作成と演算 #

import numpy as np

長さが N で要素がすべて0のベクトルや1のベクトルは np.zeros(N), np.ones(N) という関数で作成します。

np.zeros(3)

np.ones(5)

`array` は、 正確には `numpy.ndarray` という型でベクトルを表します。 (今は割愛しますが、本来は、行列やテンソルも表します)

区間 [left, right] について、均等な幅で N個の点の列を作るには、 np.linspace(left, right, N) を使います。

np.linspace(21, 30, 10)

演算 #

ベクトルに対して、主に2種類の演算を使います。

(1) 同じ長さのベクトル同士の四則演算は、各要素毎に行われます

np.ones(3) + np.ones(3)

積の例 $\quad (1, 2, 3) * (1, 2, 3) \to ((1 \cdot 1), (2 \cdot 2), (3 \cdot 3)) \to (1, 4, 9)$

np.linspace(1, 3, 3) * np.linspace(1, 3, 3)

(2) 数 (スカラー) とベクトルの四則演算は、ベクトルの各要素とスカラーの演算を行います。これは関数を作成するときに便利です。

np.ones(3) * 2

np.ones(3) * 2 + 10

関数 #

例として数学関数 $f(x) = x^2 + 1$ を $x \in \{1,2,3\}$ の各点について、1度に計算してみましょう。

def f(x):
    return x ** 2 + 1

f(0)

x = np.linspace(1,3,3)

x

f(x)

グラフを描く #

import matplotlib.pyplot as plt

上記のコードのようにPython の matplotlib.pyplot というモジュールを plt という名前で使います。正確に import してください。これが標準的な使い方になっているので、合わせましょう。

グラフの書き方は、plt.plot(x, y) で、引数の x と y は同じ長さのベクトルを表す式を渡します。 早速描いてみましょう。

plt.plot(x, f(x))

3点を線でつないだグラフが表示されました。 2次関数を把握できるように、点の数や区間を調整してみましょう。x を、たとえば区間 [0,5] で等間隔の 50点の列に変更して再度描画すると、見慣れた曲線になります。

x = np.linspace(0, 5, 50)

plt.plot(x, f(x))

なお、数が50の時は省略できます。つまり、np.linspace(0, 5, 50) と np.linspace(0, 5) は同じです。

最後に、このページ冒頭の softplus 関数の定義の例を示します。

def softplus(x):
    return np.log(1 + np.exp(x))

数学関数は math のものの代わりに np のものを使います。つまり、 math.log の代わりに np.log を、math.exp の代わりに np.exp を使ってください。np.sin なども同様です。 この置き替えで、x がベクトルの時に、まとめて計算することができます。

複数の関数の描画 #

複数の関数を1枚のグラフに描画することもできます。

例として次の問題を考えてみましょう
$d = 0, 1, 2, \cdots$ に対して、以下の関数を定義する: $f_d(x) = (-1)^d \cdot \frac{2}{\pi} \cdot \frac{\cos((2d+1)x)}{2d+1}.$ この関数を組み合わせた $F_N(x) = f_0(x)+f_1(x)+f_2(x)+\cdot +f_N(x)$ を考えると、大きなNに対して、 $F_N(x)$ の概形はどのような形か?

Python で、小さな d についてのグラフを描いて予想してみましょう。

x = np.linspace(-math.pi, 
                math.pi)

$d=0$ をまず描いてみます。

def f0(x):
  return 2/math.pi*np.cos(x)

plt.plot(x, f0(x))

$d=1$ も同様に描けます。

def f1(x):
  return -2/math.pi*np.cos(3*x)/3

plt.plot(x, f1(x))

$F_1(x) = f_0(x) + f_1(x)$ も、 次のように簡潔に書くことができます。 f0(x)+f1(x) がPythonの式であることと対応しています。

plt.plot(x, f0(x)+f1(x))

同様に `f_2(x)` を作成後に、3つの関数を描いてみます。`plt.plot` を続けて描くと、複数の関数を1枚のグラフに描くことができます。形が見えてきました。

plt.plot(x, f1(x))
plt.plot(x, f1(x)+f2(x))
plt.plot(x, f1(x)+f2(x)+f3(x))

少し応用的な文法になりますが、グラフに凡例を付与することもできます。

plt.plot(x, f1(x), 
         label='1')
plt.plot(x, f1(x)+f2(x), 
         label='1+2')
plt.plot(x, f1(x)+f2(x)+f3(x),
         label='1+2+3')
plt.legend()

授業などで、新しい関数を目にしたら、まずは概形を描いてみましょう。 実測データのときでも、グラフの書き方は基本は同じなので、データの読み込み方を習得すれば図示できます。

グラフのファイルへの保存 #

グラフを pdf で保存するには、描画直後 (同じセルの中) に以下の文を加えます。

# 実際のグラフを描くコード (省略)
plt.savefig('filename.pdf')

ファイルを見つけたら、右クリックからダウンロードします。

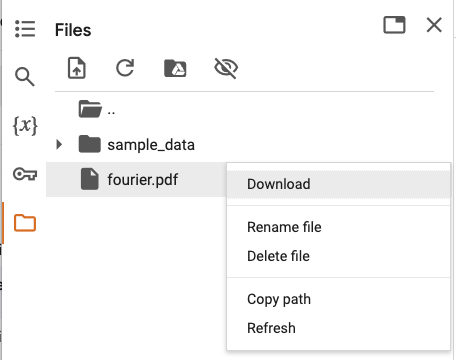
ファイルの保存直後は、ファイル一覧に現れないかもしれません。その場合は、上部のリロードボタン (回転する矢印) を押すと一覧が更新されます。

保存されたファイルが真っ白 --- `plt.savefig('filename.pdf')` を別のセルで動かすと、描画内容が消去されてしまっているかもしれません。少し複雑になりますが、`plt.figure()` を利用して今描画中の図を変数で参照できるようにすると、別のセルから保存することもできます。

fig = plt.figure()
# 実際のグラフを描くコード (省略)
fig.savefig('filename.pdf')